Sur la matière - III
Tout ce que vous
avez toujours
voulu savoir sur la matière sans
oser le
demander – Part-III
Nguyễn Quang
5-De la MQR à la QFT
Malgré les succès obtenus, la mécanique quantique relativiste (MQR en abrégé) souffrait d’une insuffisance majeure : avant la «seconde quantification» effectuée par Dirac, elle ne pouvait décrire que des systèmes où intervient un nombre fixé de particules, et sans interaction entre elles ; en particulier lui échappait le mécanisme détaillé des processus d’annihilation ou de création de particules, alors même que, paradoxalement, c'était la relativisation de la MQ par Dirac qui avait amené la découverte de l'anti-matière. Il fallait pallier ce défaut, ne fût-ce que pour mettre de l’ordre dans la ménagerie de particules «élémentaires» (on en comptait plus de 400 au début des années 1950!) qui proliférait avec le développement d’accélérateurs de plus en plus puissants, et dont Enrico Fermi disait en plaisantant : « Si je pouvais mémoriser tous les noms dans ce bestiaire, je serais zoologiste, pas physicien! » (tableau 5.1). N’empêche qu’on pouvait s’inspirer de la méthode première des sciences naturelles, la classification, pour essayer de mettre empiriquement en évidence des structures cachées (comme Mendeleïev l’avait fait dans le tableau périodique des éléments). L’étude de la «force de liaison» du noyau atomique et de la désintégration bêta avait accrédité l’idée qu’aux deux types d’interaction connus de la physique classique, la gravitation et l’électro-magnétisme, il convenait d’en ajouter deux autres : les interactions forte et faible, dont la portée et l’intensité sont récapitulées dans le tableau 5.1.
Il est à noter que ce qui justifie l’appellation (forte ou faible) de ces interactions, c’est bien sûr leur intensité, mais aussi la probabilité avec laquelle elles se manifestent : la probabilité de provoquer une réaction nucléaire en bombardant un noyau par des particules alpha (comme dans les expériences de Rutherford) est forte ; plus faible est la probabilité de désintégration qui intervient dans la radioactivité bêta, comme le montre la durée de demi-vie du neutron, qui est d’ordre macroscopique (une quinzaine de minutes). L’ensemble des quatre interactions fondamentales est censé gouverner et expliquer la totalité des phénomènes physiques connus, étant entendu que les forces gravitationnelles sont négligeables aux niveaux atomique et subatomique. Une première taxinomie distingue alors trois familles : le photon, soumis à l’interaction électromagnétique ; les hadrons, à l’interaction forte ; les leptons, à l’interaction faible, et aussi à l’interaction électromagnétique (neutrinos exceptés). Puis les hadrons sont divisés en deux sous-familles classées suivant leurs spins : les baryons (lourds) avec spin = 1/2 ou 3/2, et les mésons (moyens) avec spin = 0 ou 1.
Des subdivisions encore plus fines font intervenir des nombres quantiques, c-à-d. des valeurs propres d’opérateurs commutant avec le hamiltonien (voir section 3), et qui caractérisent des propriétés invariantes dans la dynamique de la particule : il y a le spin, qui différencie les bosons des fermions (section 4), mais aussi la «couleur», le «charme», la «saveur», «l’étrangeté»… On soupçonnait naturellement que dans cet inventaire à la Prévert, beaucoup de particules «élémentaires» ne l’étaient pas et résultaient, par des processus d’interaction, de particules fondamentales en nombre plus restreint. C’est ce que révèle le tableau 5.3, qui récapitule les constituants ultimes (à ce jour) de la matière et leurs interactions, et où le boson BEH vient enfin de prendre sa place.
| Interaction |
Théorie courante |
Médiateurs |
Masse (GeV/c2) |
Puissance relative approxi- mative |
Rayon d'action (m) |
Dépen- dance de distance |
| Forte |
Chromo- dynamique quantique (QCD) |
8 gluons | 0 | 1 | 2,5·10−15 | \(\frac{1} {r^7}\) |
|
Électro- magnétique |
Électro- dynamique quantique (QED) |
photon | 0 | 10-2 |
∞ |
\(\frac{1} {r^2}\) |
| Faible | Théorie électrofaible | W+, W-, Z0 | 80, 80, 91 | 10-13 |
10−18 |
\(\frac{1} {r^5}\) à \(\frac{1}{r^7}\) |
| Gravitation |
Relativité générale |
graviton (postulé) |
0 |
10-38 |
∞ | \(\frac{1} {r^2}\) |
Tableau 5.1 Tableau récapitulatif des 4 interactions fondamentales

Tableau 5.2 Tableau des particules élémentaires dans les années 1950

Tableau 5.3 Les particules élémentaires du modèle standard
Mais, comme nous en avions averti le lecteur, le dévoilement précoce du dénouement ne fait qu’apporter son lot de questions – toutes les questions en fait qu’a dû résoudre la théorie quantique des champs (en abrégé QFT, quantum field theory) succédant à la mécanique quantique relativiste (MQR), sous ses formes successives/complémentaires, de la QED (quantum electrodynamics) à la QCD (quantum chromodynamics), des symétries de jauge à la brisure spontanée de symétrie. Nous touchons ici aux limites de nos efforts de vulgarisation car, quand les concepts n’ont plus d’analogues en physique classique (voir par exemple les nombres quantiques), le langage mathématique seul permet de les définir correctement. Le langage intuitif conserve son pouvoir de suggestion, mais la rançon en est l’imprécision, et parfois la confusion engendrée par de fausses analogies.
La seconde quantification
Avant d’empiler encore des axiomes sur les six postulats de la section 4, il convient d’examiner d’abord, pour leur valeur heuristique, les deux premières ébauches de description des interactions faible et forte proposées respectivement par Fermi et Yukawa en 1934 et 1935 :
– Dans la radioactivité bêta, un neutron se transforme en un triplet proton + électron + neutrino, le couple proton + électron assurant la conservation de la charge et le couple proton + neutrino la conservation de la masse. Notons qu’à l’époque, le neutrino n’était qu’une particule hypothétique inventée par Pauli, de masse infinitésimale (mais non nulle), donc particulièrement difficile à détecter ; elle ne sera mise en évidence qu’en 1956. Les premières explications du mécanisme bêta sous-entendaient que l’électron préexistait au sein du noyau. En complète rupture avec ce présupposé, dans le modèle que propose Fermi (prix Nobel 1938), ni l’électron ni le neutrino ne préexistent, ils sont créés dans une interaction «de contact» à quatre fermions, plus précisément entre deux couples fermion-antifermion. La théorie de Fermi peut être considérée comme une approximation (à basse énergie) de la QED, la théorie unifiée électrofaible du modèle standard, à condition de remplacer les interactions «de contact» par des interactions transmises par l’échange d’un triplet de bosons W intermédiaires (voir ci-dessous).
– Justement, le modèle proposé par Yukawa (prix Nobel 1949) explique la cohésion du noyau par l’échange entre les nucléons d’une particule hypothétique, le méson π ou pion, d’une masse approximativement égale à 200 fois celle de l’électron, et mise en évidence en 1947. Dans la théorie QCD du modèle standard, le méson est le quantum du champ d’interaction forte. Quand elle est échangée, cette particule est délocalisée, un peu comme le chat de Schrödinger, et le postulat de la «réduction du paquet d’onde» implique que sa détection interrompt sa transmission entre les nucléons concernés. Le principe d’indétermination de Heisenberg permet alors d’enfermer les variations d’énergie (donc de masse) et de temps de parcours de la particule-énergie (voir section 2) dans une «boîte» dont les dimensions sont dictées par la constante de Planck. C’est ainsi qu’à partir de la taille de l’atome, Yukawa a pu estimer la masse de son méson.
Ces deux ébauches de QFT font apparaître le principe fondamental de création/annihilation de certaines particules à la suite d’interactions entre des champs. C’est une sorte de réponse au rêve unitaire d’Einstein (formulé dans la section 3) : «Dans sa forme mature, l’idée de la QFT est que les champs quantiques sont les ingrédients de base de l’univers, et que les particules ne sont que des paquets d’énergie et de moment de ces champs […] La QFT a donc conduit à une vue plus unifiée de la Nature que la vieille interprétation dualiste en termes à la fois de particules et de champs» (S. Weinberg, prix Nobel 1979).
Place maintenant au formalisme de la «seconde quantification», que les insuffisances du langage non mathématique, ainsi qu’on l’a signalé, rendront nécessairement plus vague et schématique que dans les sections précédentes.
Une première étape consiste à interpréter la donnée des vecteurs d’état et des observables (section 4) comme la donnée de champs, au sens de la section 3, définis en chaque point du continuum espace-temps. On les appellera d’une façon générale des champs quantiques. Notons qu’alors le principe de superposition de la MQR (postulat 1), d’arbitraire devient naturel, puisque par définition même, les champs se superposent. Dans une seconde étape, il faut introduire des opérateurs de champ, définis, pour des raisons de commodité mathématique, non pas en termes spatio-temporels, mais en termes de moments conjugués dans l’espace de configuration (section 3). En quelque sorte, on pourrait dire que, comme la MQR a quantifié la mécanique rationnelle, la QFT va quantifier la mécanique analytique. Les moments conjugés du formalisme lagrangien sont remplacés par des opérateurs qui représentent des observables comme en MQR, et qui vont obéir à des relations de commutation (section 4) dépendant, bien sûr, de l’interprétation physique de ces moments.
Difficulté technique : sur quel espace de Hilbert ces opérateurs de champ vont-ils agir ? Comme les particules du système étudié sont de différentes espèces et peuvent varier en nombre, l’espace de référence doit non seulement comprendre tous leurs espaces d’états, mais aussi tenir compte de leurs différents comportements statistiques (Bose-Einstein/Fermi-Dirac).
Un espace adéquat existait déjà en physique statistique, l’espace de Fock. Adapté au cadre quantique, il va se présenter comme une superposition infinie (mathématiquement, une somme directe de produits tensoriels) de tous les espaces d’états des particules du système, auxquels on applique au préalable un opérateur qui les symétrise ou les antisymétrise suivant qu’il s’agit de bosons ou de fermions. L’espace de Fock est quantifié par des nombres d’occupation, qui en donnent une base commode et sont définis comme suit : dans un espace d’états donné d’une population de particules identiques, admettant une base \(|\psi_j\rangle\), le nombre d’occupation |n0, n1,…, nk> désigne l’état correspondant à n0 particules dans l’état \(|\psi_0\rangle\),…, nk particules dans l’état \(|\psi_k\rangle\). Par convention, \(|0\rangle\) désigne l’état du «vide», qui est l’état de plus bas niveau d’énergie (et non le néant!).
L’espace de Fock est l’espace de représentation de la phénoménologie quantique, sur lequel les opérateurs de champ vont agir en provoquant des événements consistant en l’émission ou l’absorption d’un quantum de champ ([CTS] p.162). Mathématiquement, ces opérateurs appartiennent donc à l’algèbre engendrée par les deux opérateurs d’annihilation et de création, notés respectivement \(a\) et \(a^\dagger\), qui sont des opérateurs adjoints au sens mathématique, et qui agissent sur un état de Fock en enlevant ou en ajoutant une particule. En particulier, dans la base des nombres d’occupation, l’opérateur d’annihilation ai agit sur |n1,…, nk> en transformant ni en ni + 1 et en laissant fixes les autres coordonnées. Les opérateurs de l’algèbre peuvent alors s’exprimer en fonction des \(a_i\) et \(a_j^\dagger\) , directement ou par transformation de Fourier. Dans le cas simple d’un «champ libre» (i.e. sans interaction), de bosons par exemple, le Hamiltonien s’écrit (où Ek est l’énergie cinétique) $$H=\sum_kE_ka_k^\dagger a_k,$$ et l’opérateur d’annihilation des bosons (où r est le vecteur position et k_i un vecteur d’onde) : $$\phi(\mathbf{r}) \equiv \sum_ie^{k_i.r}a_i.$$
Dans une interaction entre champs, le passage de l’espace de Fock des champs libres entrants à celui des sortants est décrit par une matrice de diffusion : les éléments matriciels sont les amplitudes (complexes) de transition, et le carré de leur module donne la probabilité des événements produits par la transition.
Ce qu’il faut retenir derrière tout ce formalisme, c’est le pas supplémentaire dans l’élimination progressive du concept de substance au profit du concept de champ, déjà relevé par Einstein et Infeld à propos de l’électrodynamique (section 3). Le champ n’est plus un simple artifice mathématique, il devient un concept premier de la physique des particules : la particule-masse/ particule-énergie de la relativité avait été occultée derrière le quantum d’action de la mécanique quantique, celui-ci s’efface à son tour pour devenir un quantum d’interaction entre des champs quantiques.
Pour illustrer ce point de vue, convenons comme [CTS] d’écrire les champs avec une majuscule et les quanta avec une minuscule (le photon est le quantum du champ Photon ; le champ Electron a pour quanta l’électron et le positon) et prenons l’exemple de l’électrodynamique quantique : «En termes de particules, [la QED] est la théorie des interactions des électrons, des positons et des photons ; en termes de champs quantiques, c’est la théorie de la propagation et du couplage de l’Electron et du Photon» ([CTS] p.192). Vers la fin de sa vie (après la seconde quantification de Dirac mais avant l’explosion des diverses QFT), Planck disait, un rien désabusé : «Pour moi qui ai consacré toute mon existence à la science la plus rigoureuse, l’étude de la matière, voilà tout ce que je peux vous dire des résultats de mes recherches : il n’existe pas de matière!» (1947)
6-Des symétries de jauge au modèle standard
En mécanique analytique comme en théorie des champs, on utilise un nombre restreint de principes fondamentaux de «symétrie» pour construire le lagrangien et en déduire des invariants dynamiques, c-à-d. des grandeurs qui se conservent lors de l’évolution du système. En QFT, c’est l’expression de ces invariants en fonction des opérateurs adjoints d’annihilation et de création qui conduit aux relations de commutation (voir section 5) caractéristiques du champ. Le mot flou de symétrie ne doit pas être pris en un sens mathématique restrictif (symétrie ponctuelle, symétrie axiale…), mais en un sens intuitif plus large : à bien y réfléchir, les diverses lois physiques qu’on a vu défiler reposent sur quelques principes de conservation étonnamment simples tels que la conservation de la masse/énergie, de la quantité du mouvement, du moment cinétique… Mais on a vu aussi que l’empirisme de ces principes se révèle dès qu’on s’avise de définir sans équivoque la quantité qui est conservée. De fait, leur conceptualisation mathématique remonte seulement au début du 20ème siècle, dans le sillage du programme mathématique d’Erlangen, avec le théorème d’Emmy Noether, puis les symétries de jauge de Hermann Weyl.
Emmy Noether (1882-1935) (1)
Le célèbre programme d’Erlangen proposé par David Hilbert et Félix Klein en 1872 proposait de fonder mathématiquement la géométrie sur les actions de groupes et les invariants par ces actions. Rappelons seulement qu’un groupe est un ensemble d’opérateurs muni d’une loi de composition * qui obéit à certaines règles telles que l’associativité (i.e. a*(b*c) = (a*b)*c), mais pas la commutativité (i.e. a*b n’est pas forcément égal à b*a) . Si l’ensemble E sur lequel le groupe G agit possède lui aussi une structure (espace vectoriel, espace de Hilbert, voir section 4), et si G respecte cette structure, on dira que G est un groupe de symétrie pour la structure de E.
Un exemple emblématique de groupe avec ses invariants est le groupe de Lorentz de la relativité restreinte. En voici un autre, élémentaire mais qui a le mérite de faire la distinction entre transformations «discrètes» et «infinitésimales» : soit E l’ensemble des points d’un plan rapporté à une origine O, et soit G le groupe des rotations de centre O au sens habituel ; E possède une structure additionnelle, la «métrique euclidienne» qui permet de mesurer la distance entre deux points ; comme G opère évidemment sur E en respectant cette métrique, G est un groupe de symétrie pour E au sens précédent, noté SO(2, R) (deux dimensions réelles) ou U(1, C) (une dimension complexe). Comme exemples d’invariants, prenons un carré et un cercle, tous deux centrés sur O. Une rotation de n’importe quel angle, aussi petit soit-il (on dit une rotation infinitésimale) conserve globalement le cercle ; en fait, ces rotations constituent le groupe G lui-même. Tandis que seules les rotations d’un angle égal à un multiple de 90 degrés conservent globalement le carré ; ces rotations discrètes forment un sous-groupe de G à 4 éléments.
Dans l’esprit du programme d’Erlangen, une étudiante de Hilbert et Klein, Emmy Noether (dont le nom reste pricipalement attaché à ses importants travaux en algèbre commutative) a démontré vers 1905 un théorème sur les invariants différentiels dans le calcul des variations qui est maintenant considéré comme « l’un des plus importants théorèmes mathématiques jamais prouvé dans l’orientation du développement de la physique moderne » (Leon Lederman, prix Nobel 1988), parce qu’il établit une relation rigoureuse, dans la dynamique d’un système, entre conservation (d’une grandeur physique) et invariance par symétrie (d’une propriété physique): « A toute transformation infinitésimale qui laisse inchangée l’intégrale d’action, correspond une grandeur physique qui se conserve ». Le renversement logique du théorème de Noether présente un intérêt heuristique considérable : si une quantité physique est conservée, alors les lois (à découvrir) qui gouvernent son comportement doivent être invariantes par une certaine transformation de symétrie continue ; si l’on parvient à mettre la main sur une telle symétrie, ou mieux, sur tout un groupe de symétrie, alors non seulement on peut écarter d’emblée de vastes éventails de structures mathématiques possibles, mais on peut aussi chercher à identifier les relations sous-jacentes entre les lois gouvernant les quantités physiques reliées à ce groupe de symétrie. C’est grosso modo la démarche des théories de jauge.
Hermann Weyl (1885-1955)
Il nous reste maintenant à expliquer ce qu’est une symétrie de jauge locale, une notion introduite (mais pas très heureusement nommée) autour de 1918 par le mathématicien allemand Hermann Weyl. Bien que connu surtout pour ses importantes contributions à la théorie des groupes de transformation continue appelés «groupes de Lie», Weyl s’était aussi intéressé à la physique théorique avec Einstein.
Son idée de départ était que les lois de conservation doivent être associées non pas à un seul groupe global de symétrie, mais à un champ de groupes locaux qui sont des copies de ce groupe, le groupe de jauge, agissant en chaque point de l’espace-temps. Pour préciser un peu, considérons la fonction d’onde \(|\psi\rangle = |\psi(\mathbf{r},t)\rangle\), où r est le vecteur de position spatiale et t le temps. L’équation de Schrödinger qui gouverne l’évolution de \(|\psi\rangle\) est manifestement invariante par un changement de phase global, c-à-d. par une transformation consistant à multiplier \(|\psi\rangle\) par un nombre complexe de module 1 (dont la phase est «l’argument», en termes mathématiques), indépendant du quadrivecteur (r,t) : c’est une invariance de jauge globale par le groupe U(1). Mais si le changement de phase dépend de (r, t), comme dans tout champ qui se respecte, l’équation de Schrödinger n’est plus invariante. Si nous particularisons \(|\psi\rangle\) en prenant la fonction d’onde classique de Maxwell, alors l’invariance de jauge locale par U(1) imposée par Weyl s’obtient en faisant apparaître une interaction entre les champs de force associés au potentiel-vecteur et au potentiel électrique. La situation se transpose telle quelle en QFT, en remplaçant les potentiels classiques par les champs Photon et Electron. Les bosons qui apparaissent lors d’une telle interaction – ici le photon – sont appelés bosons de jauge (voir tableau 5.3).
L’ambition de Weyl était d’unifier l’électrodynamique et la relativité générale en assignant une invariance de jauge à l’espace lui-même. Cette idée ne marcha pas pour la gravitation, mais c’est elle qui est à l’œuvre derrière les théories de jauge qui ont réussi successivement à élucider les interactions faible et forte, et même à unifier la première avec l’interaction électromagnétique. Leur synthèse constitue le grandiose «modèle standard», qui unifie toutes les interactions fondamentales en dehors de la gravitation (le domaine de la relativité générale).
Les théories de jauge
On donne ci-dessous un tableau récapitulatif des diverses théories de jauge qui culminent dans le modèle standard, ainsi que des groupes de jauge qui leur sont associés. Fait notable, ces théories n’ont pas progressé séparément mais de concert, s’alimentant l’une l’autre, nécessitant chacune des années d’efforts acharnés, conjoints ou croisés (voir [B]). Elles ont rapporté leur moisson de prix Nobel, mais elles ont surtout justifié, comme jamais, la phrase de Newton : «Si j’ai pu voir aussi loin, c’est que je suis monté sur les épaules des géants qui m’ont précédé».
| Electrodynamique quantique QED | Groupe U(1) | Force électromagnétique |
| Théorie unifiée électrofaible | SU(2)xU(1) | Forces é-m. et faible |
| Chromodynamique quantique QCD | SU(3) | Force forte |
| Modèle standard | SU(3)xSU(2)xU(1) | 3 forces unifiées |
Un minimum d’explications s’impose. D’abord les groupes : tous les scalaires étant des nombres complexes, on sous-entend la notation C précédemment introduite ; U(n) désigne alors le groupe des opérateurs (appelés unitaires) qui conservent la structure d’un espace hilbertien de dimension finie n, et SU(n) le sous-groupe formé des opérateurs unitaires de déterminant égal à 1. Même l’homme de la rue connaît U(1), qui n’est autre que le groupe des phases, i.e. des angles considérés à 360 degrés près (mathématiquement, on dit modulo 2π), qu’on additionne/retranche modulo 2 pi. Parmi tous les U(n), seul U(1) est commutatif (on dit aussi abélien).
Puis les interactions : on a vu que U(1) se présente comme le groupe de jauge naturel de l’électrodynamique classique. Il reste celui de l’électrodynamique quantique (on remarquera que QED est aussi l’acronyme de la locution latine signifiant «ce qu’il fallait démontrer» ; les scientifiques sont friands de ce genre de jeu de mots), mais la quantification du champ électromagnétique présentait des difficultés en apparence insurmontables, même pour Einstein, qui s’en tirait par cette boutade : « Dieu semble avoir trouvé un truc » (1910). Le truc, c’est comment étendre à un champ quantique la notion d’intégrale d’action – classiquement, l’intégrale du lagrangien sur l’espace de configuration – de façon à pouvoir appliquer un principe de moindre action, comme en mécanique analytique et en optique ondulatoire. C’est ce qu’a fait Feynman dans un article de 1948 où il introduit l’intégrale de chemin (à ne pas confondre avec les intégrales curvilignes de la physique classique) :
il ne cherche plus à calculer la probabilité pour qu’une particule se trouve en un certain point spatio-temporel, mais la probabilité pour qu’elle emprunte une trajectoire (un «chemin» ou une «ligne d’univers») contenue dans une certaine région de l’espace-temps ; en postulant que la contribution d’un chemin possible est l’exponentielle de i fois l’action classique (ce qu’on appelle une «pure phase»), il montre que la somme des contributions de tous les chemins qui, partant du passé, aboutissent au point (r,t) n’est autre que la fonction d’onde \(|\psi(\mathbf{r},t)\rangle\) qui vérifie l’équation de Schrödinger ([CTS], p.187).
Disons tout de suite que le «truc» de Feynman, même s’il était trop beau pour ne pas être vrai, n’était pas assuré mathématiquement :
dans son intégrale de chemin, la variable d’intégration ne vit plus dans un des espaces habituels de la théorie de l’intégration, elle se balade dans un espace incommensurable de fonctions, d’où un problème de «divergence», c-à-d. que l’intégrale à calculer peut devenir infinie ! Pour l’approcher, on utilise en pratique un développement perturbatif, c-à-d. un développement en série suivant les puissances de la constante de couplage entre les champs en interaction, et dont les coefficients n’impliquent que des intégrales au sens habituel. Les diagrammes de Feynman donnent des recettes pour calculer ces coefficients, mais dans un certain nombre de cas où ces diagrammes sont «en boucle», l’intégrale de chemin est effectivement divergente.
Le remède consiste en un procédé très technique de renormalisation (Feynman, Schwinger, Tomonoga, prix Nobel 1965) qu’il n’est pas utile de détailler ici, sauf pour dire que la situation n’était pas tout à fait satisfaisante : il fallait montrer au cas par cas, pour chaque théorie de jauge, que la renormalisation était possible. Jusqu’à ce qu’en 1972, ‘t Hooft et Veltman (prix Nobel 1999) prouvent que toutes les théories de jauge de Yang-Mills avec « brisure de symétrie » (voir plus bas) sont renormalisables.
Le succès de la QED, qui arrivait à prédire des résultats expérimentaux avec une exactitude ahurissante (pour le «facteur de Landé» de l’électron, avec une précision équivalente à l’épaisseur d’un cheveu sur la distance de Los Angeles à New York !) ne pouvait qu’inciter les chercheurs à chercher des théories de jauge analogues, mais non abéliennes (c-à-d. associées à des groupes de jauge non commutatifs).
Celle de Yang et Mills, établie au début des années 1950 pour rendre compte de l’interaction forte, s’applique en fait à tous les groupes de Lie compacts semi-simples, c’est pourquoi l’on en parle couramment au pluriel. Au départ, Heisenberg avait émis l’hypothèse que le proton et le neutron s’associent dans le noyau en échangeant un électron, et introduit l’idée d’isospin (un analogue du spin, mais un analogue seulement) pour distinguer entre les deux états de la particule neutron / proton. Yang et Mills identifièrent l’isospin comme une symétrie de jauge locale, à l’image de la symétrie U(1) dans la QED, mais avec deux particules en jeu, il fallait élargir le groupe de jauge. En optant pour SU(2), ils furent amenés à introduire un nouveau champ, baptisé B, accompagné de trois particules de jauge, baptisées B+ (pour l’interaction proton-neutron), B- (pour l’interaction inverse) et B° (pour l’interaction neutron-neutron). Le lecteur aura reconnu en passant l’intervention des opérateurs de création/annihilation. Mais ce modèle ne marchait pas, d’une part parce qu’il n’était pas renormalisable, d’autre part parce que le terme zéro du développement perturbatif indiquait des masses nulles pour les particules médiatrices, donc une interaction de portée infinie (voir la section 5 à propos de la masse du méson), en totale contradiction avec l’interaction forte (2).
Mais le plan de marche de Yang et Mills demeurait valable, à condition de changer de groupe de jauge. Le problème devait être résolu par la QCD proposée en 1973 par Gross, Politzer et Wilczek (prix Nobel 2004), une théorie de jauge SU(3) : l’interaction forte est due à l’échange de couleurs entre les quarks par le biais de gluons.
Pour éviter l’exclamation «Abracadabradantesque!», empressons-nous de dire que les quarks, une invention de Gell-Mann (prix Nobel 1969) et un jeu de mots tiré du «Finnegan’s Wake» de J. Joyce, sont les composants ultimes des hadrons ; les gluons sont les particules de jauge SU(3), des bosons de masse nulle, au nombre de 8 (= la dimension du groupe de Lie SU(3)) ; les 3 couleurs (bleue, rouge, verte) sont des nombres quantiques (voir section 5), appelées charges de couleur par analogie avec les charges électriques de la théorie électrofaible ; des particules «chargées» interagissent en changeant de couleur, la couleur blanche, combinaison des 3 couleurs fondamentales, étant la seule neutre ; le problème de la portée d’interaction liée aux masses nulles est évacué par la nature particulière de la force d’attraction des couleurs, qui augmente avec la distance et confine les quarks au sein des hadrons. Comme le présent exposé est centré sur le boson BEH, ne nous attardons pas plus sur l’interaction forte et passons directement à l’interaction faible.
Vers la fin des années 1950, l’analogie (mais une analogie seulement) entre l’hypothèse de Heisenberg et la désintégration bêta (voir le début de la section 5) avait conduit Schwinger (prix Nobel 1965 avec Feynman et Tomonoga, voir plus haut) et son étudiant Glashow, indépendamment de Yang et Mills, à introduire trois particules, les trois bosons de l’isospin faible W+, W- et Z° (dans la terminologie actuelle) pour rendre compte de l’interaction faible. La présence de charges électriques suggérait aussi qu’il fallait d’emblée échafauder une théorie unifiant la force faible et la force électromagnétique, ce qu’on appelle maintenant la théorie électrofaible. Glashow opta pour le groupe de jauge SU(2)xU(1), mais se heurta aux mêmes obstacles que Yang et Mills, à savoir un modèle non renormalisable, avec des particules médiatrices de masse nulle. Comment donner une masse matérielle à des particules de masse nulle ? La solution devait venir de la théorie de brisure spontanée de symétrie de Nambu (prix Nobel 2008) et Goldstone, complétée par le mécanisme BEHGHK qu’on examinera plus loin. Appliquée à la théorie de jauge SU(2)xU(1) de Glashow, elle permit à Abdus Salam et Steven Weinberg, indépendamment, de parachever en 1967 la théorie électrofaible unifiée pour les leptons : la «projection» sur U(1) fait retrouver la QED, la brisure de symétrie permet d’attribuer une masse aux bosons W+, W- et Z° (environ 85 fois la masse du proton pour W, 96 fois pour Z), et même de prédire l’apparition d’une quatrième particule matérielle, le boson BEH. Le trio Glashow-Salam-Weinberg fut récompensé par le prix Nobel en 1979, bien avant que les trois premiers bosons fussent mis en évidence en 1983 par l’accélérateur LEP du CERN. Quant au dernier, sa détection par le LHC fait partie de l’actualité.
Lorsque le boson paraît…
La brisure spontanée de symétrie d’un système est un phénomène fréquent en mécanique statistique, qui résulte d’un conflit entre la stabilité de l’état fondamental (celui de plus basse énergie) et la symétrie de la dynamique du système, sous l’effet de fluctuations incontrôlables (thermiques, quantiques) qui n’ont pas la symétrie en question. Imaginons par exemple une bille posée en équilibre au sommet d’un sombrero mexicain (fig. 6.1), dont la symétrie globale est de révolution ; le sommet est un état symétrique d’énergie extrémale, mais instable ; la rigole du chapeau est un état de même énergie, mais stable ; une fluctuation dynamique (soleil, vent, tremblement) peut briser l’équilibre et faire rouler la bille dans la rigole sans dépenser d’énergie : c’est une brisure spontanée de symétrie.
Dans les théories quantiques le vide est l’état fondamental, celui de plus basse énergie. Quand il y a plusieurs états vides possibles, les uns stables mais non symétriques localement, les autres instables mais symétriques globalement, on peut «changer de vide» sans dépenser d’énergie, mais le principe de Nambu-Goldstone (1956) stipule qu’un tel changement fait apparaître un quantum d’un champ de matière qui est une particule ayant les nombres quantiques du vide, neutre, de spin zéro, sans masse, le boson de Nambu-Goldstone. Lorsque la symétrie qui est spontanément brisée est une symétrie abélienne de jauge locale (la composante U(1) du groupe de jauge SU(2)xU(1)), le passage d’un vide symétrique à un vide non symétrique doit correspondre à un changement de jauge. Que devient le boson de Nambu-Goldstone dans ce changement ? L’invariance de jauge locale (voir le début de cette section) nécessite, pour que la symétrie de jauge U(1) de la QED soit conservée, une interaction avec un autre champ, le champ BEH. C’est la mise en branle du mécanisme BEH, les quanta du champ BEH se combinant aux bosons sans masse de Nambu-Goldstone pour donner un photon et quatre bosons massifs, W+, W-, Z° et le boson BEH.
Le bilan, assez compliqué quand même, est schématisé dans la fig. 6.2. Notons que, dans son étude de la brisure de symétrie, Nambu avait déjà eu l’intuition d’une sorte de champ Deus ex machina : «Que se passerait-il si une sorte de matériau supraconducteur emplissait tout l’Univers, et que nous vivions dedans ? Puisque nous ne pouvons pas observer le véritable vide, l’état fondamental de ce milieu deviendrait, en réalité, le vide. Mais alors, même les particules qui seraient sans masse […] dans le véritable vide acquerraient une masse dans le monde réel». Ce n’était que spéculation (3) , mais après tout, les articles originaux de Brout-Englert et de Higgs (1964) faisaient chacun … une page et demi seulement !
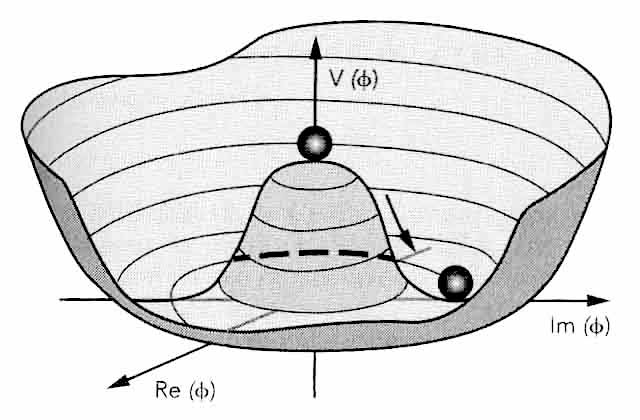
Fig. 6.1 Potentiel d’auto-interaction du champ BEH en forme de sombrero
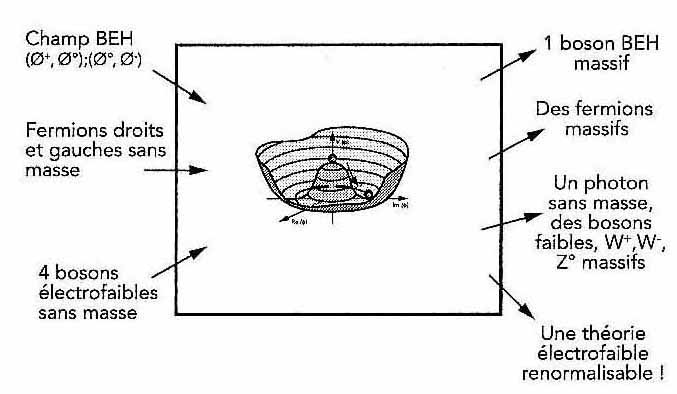
Fig. 6.2 Bilan schématisé du mécanisme BEH
Pour ne pas laisser le lecteur sur sa faim, on peut décrire par analogie le mécanisme BEH comme l’a fait le physicien David Miller en 1990 (cité dans [B]) pour rallier au projet LHC du CERN les politiciens britanniques de l’époque. Miller les mettait en scène avec Mme Thatcher, mais imaginons plutôt la réception mondaine lors de la remise du prix Nobel, avec des invités uniformément répartis dans la salle. Arrivent les lauréats, Higgs en tête, qui essayent de se frayer un chemin à travers ce «champ». Les invités s’agglutinent autour d’eux, ralentissant d’autant leur progression : cela revient à donner une masse à des bosons originellement sans masse. Dans le même temps, la rumeur de la présence des lauréats se répand dans la salle, provoquant des attroupements au fur et à mesure qu’elle se propage : c’est le boson BEH qui apparaît dans le «champ».
Nous sommes ainsi arrivés au terme de la construction de la théorie unifiée électrofaible, dont le boson BEH constitue la clé de voûte. On voit dans le diagramme d’interactions de la fig. 6.3 que le BEH donne aussi leur masse au quarks, ce qui justifie le commentaire du comité Nobel selon lequel «nous n’existerions pas sans [ce boson]».
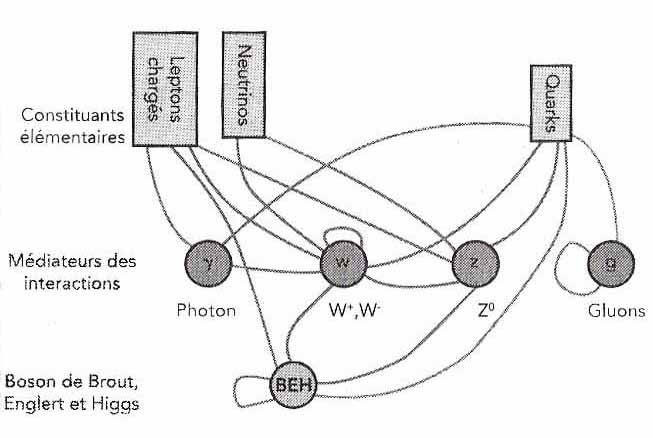
Fig. 6.3
Interactions du modèle standard
électrofaible
Les
particules avec lesquelles le boson BEH interagit directement
acquièrent une masse. Mais les neutrinos aussi sont massifs
Mais est-ce pour autant la clé ultime, la «particule de Dieu» ? Le modèle standard, la théorie de jauge U(1)xSU(2)xSU(3) qui coiffe toutes les autres théories de jauge, n’a pas encore achevé sa maturation : il présente encore trop de degrés de liberté (19), à l’encontre du «principe de parcimonie» (ou «rasoir d’Occam») ; des phénomènes tels que la masse du neutrino lui échappent ; le «confinement» des quarks attend encore une modélisation mathématique (qui fait partie d’ailleurs de l’un des 7 Problèmes du Millénaire, dotés chacun d’un million $ par l’Institut Clay) ; surtout, l’interaction gravitationnelle (la relativité générale) lui reste étrangère. Sans même parler des problèmes cosmologiques, on attend encore une dernière synthèse, une «théorie du tout» (GUT) qui expliquerait… tout. Dans l’intervalle, et à une époque où l’idéologie marchande prétend se poser en horizon indépassable de la société humaine, il est réconfortant de voir que tant de talents, parfois de génies, persistent à s’engager, individuellement ou collectivement, sur les chemins ardus de la connaissance. ¤
Nguyễn Quang
Crédit images : toutes les illustrations sont tirées de Wikipédia, sauf les figures 6.1, 6.2, 6.3 qui sont extraites du chapitre 7 de [CTS].
(1) Einstein saluait Emmy Noether comme «le plus grand génie mathématique créatif qu’ait produit l’éducation supérieure des femmes depuis qu’elle existe». Mais en dépit de cette renommée, elle n’a jamais obtenu de poste universitaire d’un niveau plus élevé que Privatdozen (assistante). La faute en revient bien sûr au sexisme de son époque. En 1900, Emmy Noether fut l’une des deux seules étudiantes admises à l’université d’Erlangen. En 1915, quand Hilbert essaya de la faire nommer à Göttingen, il se heurta à des objections du style : «Que diront nos soldats quand ils reviendront à l’université et seront obligés d’apprendre sous le joug d’une femme?» Réplique de Hilbert : « Nous sommes à l’université, pas aux bains-douche! »
(2) La petite histoire raconte que Yang exposa sa théorie en 1954 au séminaire «shotgun» de Princeton, ainsi nommé parce que les conférenciers s’y faisaient «massacrer» plus souvent qu’à leur tour. Ce qui ne manqua pas, puisque Pauli harcela Yang de questions sur la masse de son fameux champ B. Au point qu’Oppenheimer dut intervenir pour que le malheureux pût poursuivre son exposé
(3) On dirait une résurgence de l’éther, mais ce n’est qu’une analogie
Các thao tác trên Tài liệu










